Typing policy
The inherit and the insert relationship
The traditional inheritance mechanism introduced from the very beginning of Eiffel is still present. Syntactically, the inherit keyword is still used and one class can have zero, one or more parents. The inherit relationship is the one to be used when there is a subtyping relationship. In the remainder, saying A inherits from B means that a path using only inherit links exists from A to B. Saying A inherits directly from B means that B is syntactically a member of the inherit list of A.
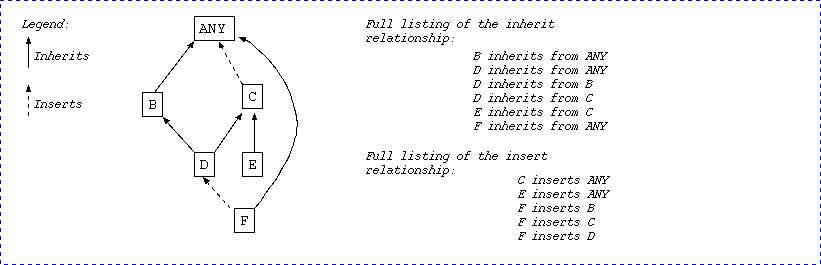
A class can also have a second parent list introduced by the insert keyword. This is the relationship to be used when code has to be inserted just for implementation purpose. The insert list can syntactically have zero, one or more parents. Saying A inserts B means that a path using insert or inherit links exists from A to B, but A does not inherit from B (i.e. at least one insertion link exists from A to B in every path). The sum of the inheritance graph and the insertion graph must be an acyclic directed graph. Saying A inserts directly B means that B is syntactically a member of the insert list of A. Following figure summarises the inheritance and insertion relationships with a complex example:
The idea behind the insertion mechanism is simple: complement the traditional inheritance mechanism with a new one that keeps the code reuse aspects but discards the subtyping relationship. As we will see in the typing and checking policy rules section, the fact that A inserts B does not allow us to assign an expression of type A into some variable of type B. For such a polymorphic assignment to be legal, A must be a subtype of B which can also be expressed as A inherits from B.
The special status of the ANY class
There is a special class in Eiffel, named ANY that has been traditionally seen as the universal ancestor of the inheritance graph. There is a special rule for the class ANY. Class ANY is the only class that has no direct ancestor at all: both its inherit list and its insert list are empty. All other classes must have at least one direct ancestor either through the inherit list or through the insert list.
Finally, class ANY is the final ancestor of the inheritance / insertion graph. As a consequence, if a class X is not the ANY class itself, then X always either inherits from or inserts ANY.
Actually, the ANY class contains important methods that all classes must have at runtime. For example, ANY contains some necessary code for object comparison (is_equal), cloning (twin) and introspection support. Thanks to the rules we have just presented, we are sure that this code is part of all Eiffel classes (i.e. reused by all classes).
Typing and checking policy rules
We will now focus on the main questions about our typing and checking policy in order to be able to answer the following crucial questions: What can be assigned into what? What type can be used when some method or attribute is overridden? What type can be used in case of a generic derivation? What about constrained genericity?
Rule 1 (Assignment)
- An expression of type A can be assigned into a variable of type B if and only if A and B are the same type or A inherits from B.
This first rule prevents an expression of one type from being assigned to a variable of another type if no subtyping relation exists between them. As a direct consequence, if A inserts B, the assignment is statically rejected and polymorphism is not possible. Furthermore, an expanded class is not allowed to inherit directly from another class (i.e. syntactically, the inherit list of an expanded class must be empty). It is also not allowed for a class to inherit directly from an expanded class (i.e. syntactically, an expanded class can only be a member of an insert list).
Rule 2 (Argument passing)
- An expression of type A can be passed as an argument of formal type B if and only if A and B are the same type or A inherits from B.
This second rule simply states that the same policy is used both for assignments (rule 1) and for argument passing (rule 2).
Rule 3 (Redefinition under Inheritance)
- When overriding an inherited method or attribute, the types of any argument and/or of its result can be replaced covariantly with a type that inherits from the replaced type (i.e. a subtype).
Actually, for inheritance, the legacy covariant principle of Eiffel is kept unchanged: all types are treated the same way (both result type and argument types), the number of arguments cannot change; if the overridden signature has a result type, the new one must also have a result type. Thus, all legacy code can be reused as is.
Rule 4 (Redefinition under Insertion)
- When overriding an inserted method or attribute, the type of any argument and/or of its result can be replaced covariantly with a type that inherits from or inserts the replaced type.
As in the case of rule 3, we assume that the overridden signature keeps the same number of arguments and that a result type cannot be discarded or added. Rule 4 is more permissive than rule 3 about the new type one can use because the overridden feature comes through a direct member of its insert list. Polymorphism between this inserted ancestor and the current type is not possible and it is thus safe to do so. This increased freedom is in fact beneficial and gives us more flexibility to adapt inserted code.
In a similar way, the exportation status of the inserted methods and/or attributes (i.e. from which other classes they are visible or can be called) can be freely changed. For example, we can insert a public attribute and convert it to a private one, or any other of the fine grained intermediate possibilities that Eiffel offers. In traditional Eiffel this was also allowed under inheritance, but this creates type safety holes in the same manner as covariant argument changing (CATCALL).
Rule 5 (Generic derivation validity)
- When deriving an actual type from a generic class, we can instantiate each parameter using any class that inserts (or inherits from) the type that constrains the corresponding placeholder. The resulting fully instantiated type is only valid if statically proven correct (recursively) with respect to all other rules.
This rule allows to instantiate a generic class using a parameter that is not a subtype of the constraining type. Both inheritance and insertion are permitted here. This can be surprising at the beginning, but is type safe, because the replacement of the formal parameter by the actual one is done at compile time and the generic derivation obtained is statically checked. In fact, polymorphism is not needed between the generic type constraint and the type that replaces it in a generic derivation. If the actual parameter is a subtype of the constraining type, the derivation will be statically valid. On the contrary, if the actual parameter only inserts the constraining type, the validity of the derivation must be checked by the compiler.
Rule 5 is meant to accept expanded types as any other parameter in classes without generic constraint like for example the ARRAY class. In this way the insertion mechanism helps us to fit non-polymorphic and efficient basic types (i.e expanded types) in a very uniform type system that maximises type combining opportunities.
Following Rule 6 and Rule 7 establish implicit inherit/insert relationships
between generic derivation of the same class.
Rule 6 (Implicit inheritance of generic derivations)
- Assuming that class G is a generic class and that G itself is not an expanded class. For two different derivations G[A1,A2,...An] and G[B1,B2,...Bn], if Bi inherits from or is equal to Ai holds for each i=1..n, then G[B1,B2,...,Bn] inherits from G[A1,A2,...,An].
Rule 7 (Implicit insertion of generic derivations)
- Assuming that class G is a generic class (expanded or not). For two different derivations G[A1,A2,...An] and G[B1,B2,...Bn], if rule 6 does not apply and if Bi inherits from, is equal to or inserts Ai holds for each i=1..n, then G[B1,B2,...,Bn] inserts G[A1,A2,...,An].
Together, rule 6 and rule 7 also state that when no relation exists for some pair (Bi,Ai), then no relation exists between both derivations of class G.